알고리즘 - 최대공약수(GCD)와 최소공배수(LCM)

최대공약수(GCD)

공통적인 약수 중 최댓값, 최대공약수가 1이면 서로소이다.

def gcd(a, b):
	ret = 0
	for i in range(min(a, b)):	# 1부터 체크
		if a % i == 0 and b % i == 0:
			ret = i
	return ret;

a의 공약수는 a보다 작고, b의 공약수는 b보다 작으므로 최소값 까지만 구하면 되기 때문에 min(a, b)까지 검사

def gcd(a, b):
	ret = 0
	for i in range(min(a, b), 0, -1):	# min(a, b)부터 체크
		if a % i == 0 and b % i == 0:
			return i

역방향으로 진행하면 O(1)만에 끝나는 경우가 있다.

유클리드 호제법

GCD(A, B) = GCD(B, A % B)

def gcd(a, b):
	return b if a % b == 0 else gcd(b, a % b)

그냥 외워버리자

최소공배수(LCM)

공통된 배수 중 최솟값 

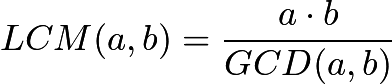
LCM(A, B) = A * B / GCD(A, B)

GCD를 구하면 LCM은 O(1)에 구할 수 있다.